\( \def\vec#1{\bf{\underline{#1}}} \)

Die Gewinnfunktion der Unternehmung ist, wie oben angegeben: \begin{equation*} G (p,\vec{w}) = \max \left(p\cdot y- \vec{w}\cdot\vec{x}\right) \end{equation*} \begin{equation*} y =f(\vec{x}) \end{equation*} Der Unternehmer will seinen Gewinn maximieren, bzw. seine Kosten minimieren. Für vorgegebenes y wird folgendes Optimierungsproblem aufstellen: \begin{equation*} min\ \vec{w}\cdot \vec{x} \end{equation*} \begin{equation*} y = f(\vec x) \end{equation*} Die Lösung dieses Optimierungsproblems ist die Kostenfunktion: \begin{equation*} C(\vec{w}, y) = min\ \vec{w}\cdot \vec{x} \end{equation*} Die Kostenfunktion gibt die Minimalkosten der Produktion $y$ an, wenn die Faktorpreise $\vec{w}$ betragen. Das Faktorbündel % $\vec{x}^*$, das die Minimierungsbedingung erfüllt, hängt also von $\vec{w}$ und $y$ ab. % \begin{equation*} \vec{x}^* = \vec{x}(\vec{w}, y) \end{equation*} Dabei heißt $\vec{x}(\vec{w}, y)$ die {\bf bedingte Faktornachfragefunktion} (bedingt durch die vorgegebene Outputmenge y).
Die Menge aller $\vec{x}(y,\vec{w})$ zu gegebenem $\vec{w}$ heißt {\bf Expansionspfad}.

Graphisch entspricht die bedingte Faktornachfragefunktion der Minimalkostenkombination.

Die Minimalkostenkombination kann sowohl als Ergebnis einer Maximierungsaufgabe, wie als Ergebnis einer Minimierungsaufgabe angesehen werden. So kommt man zur Dualität vom primalen und dualen Problem.
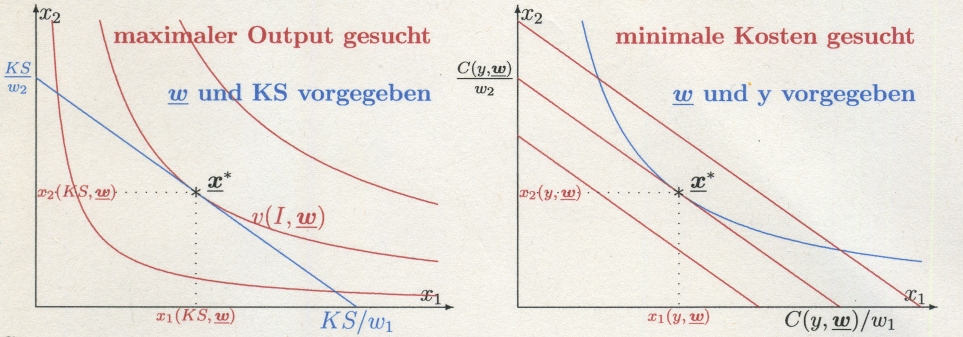
Primales Problem
Zu einer gegebenen Kostensumme (KS) wird der maximale Output gesucht. \begin{equation*} \begin{matrix} Zielfunktion \ \ \ \ f(\vec{x})&\rightarrow &\max &&&\cr Nebenbedingung \ \ \ \ \vec{w} \cdot \vec{x} &\le &KS \end{matrix} \end{equation*} 		Duales Problem
Zu einem gegebenen Output (y) werden die minimale Kosten gesucht.                                         \begin{equation*} \begin{matrix} Zielfunktion \ \ \ \ \ \vec{w} \cdot \vec{x} &\rightarrow &\min&&& \cr Nebenbedingung \ \ \ \ \ f(\vec{x}) &\ge &y \end{matrix} \end{equation*}

Die bedingte Faktornachfragefunktion $\vec{x}(y, \vec{w})$ ist Lösung des Optimalproblems:

\begin{equation*} x^*_1 (KS, \vec{w}), \ \ x^*_2 (KS, \vec{w}) \end{equation*}                                                                                                                                                                                                 \begin{equation*} x^*_1 (y, \vec{w}), \ \ x^*_2 (y, \vec{w}) \end{equation*}


Primales und duales Problem
Satz
Es sei $\vec{x}^*$ Lösung des primalen Problems und es gelte $KS = \vec{w} \cdot \vec{x}^*$. Dann ist $\vec{x}^*$ auch Lösung des dualen Problems.
Beweis
Das primale Problem ist die Gewinnmaximierung (Output Maximierung). Die Lösung des primalen Problem ist $\vec{x}^*$. Es wurde angemonnen, dass $KS = \vec{w} \cdot \vec{x}^*$ ist. Das ist die Nebenbedingung für Kostenminimierung (duales Problem). Wenn diese Annahme gilt, führen Gewinnmaximierung und Konstenminimierung zum gleichen Ergebnis: $\vec{x}^*$

Angebotsfunktion und Faktornachfragefunktion

Aus der Gewinnmaximierungshypothese des Unternehmens lassen sich Angebots- und Faktornachfragefunktion ableiten. \begin{equation*} max (p\cdot y - \vec{w} \cdot\vec{x}) \end{equation*} unter der Nebenbedingung \begin{equation*} y=f(\vec{x}) \end{equation*} oder zusammengefasst \begin{equation*} max (p\cdot f(\vec{x}) - \vec{w} \cdot\vec{x}) \end{equation*} Ist zu gegebenen $(p, \vec{w}$) das Bündel $\vec{x}^*$ die optimale Faktornachfrage, so ist die Faktornachfragefunktion \begin{equation*} \vec{x}(p, \vec{w}) = \vec{x}^* \end{equation*} und die Angebotsfunktion \begin{equation*} y(p, \vec{w}) = f(\vec{x}( p, \vec{w})) \end{equation*} Eine notwendige Bedingung für den kostenminimierenden Unternehmer finden wir durch die Optimalitätsbedingung. \begin{equation*} {w_i \over w_j} = {\partial f / \partial x_i \over \partial f / \partial x_j} = - {d x_j \over dx_i} \end{equation*} Das Faktorpreisverhältnis ist gleich dem Verhältnis der Grenzproduktivitäten und gleich der reziproken negativen Substitutionsrate.