Fall 1: $a > 0, \ b>0$ (Beispiel: $y= 1\cdot x_1^2 + 2\cdot x_2^2$)

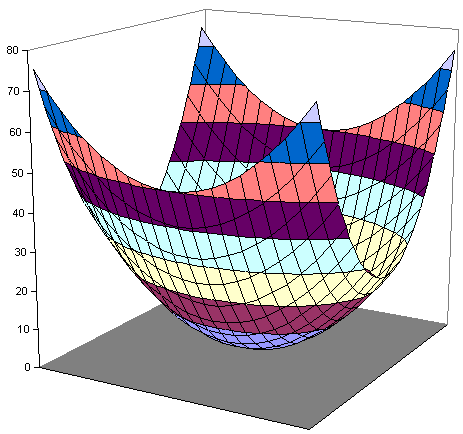
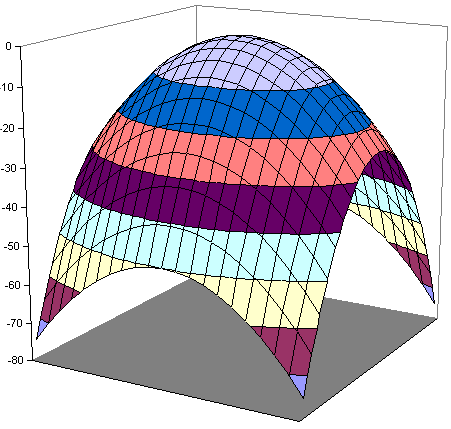
Fall 2: $a < 0, \ b<0$ (Beispiel: $y= -1\cdot x_1^2 - 2\cdot x_2^2$)

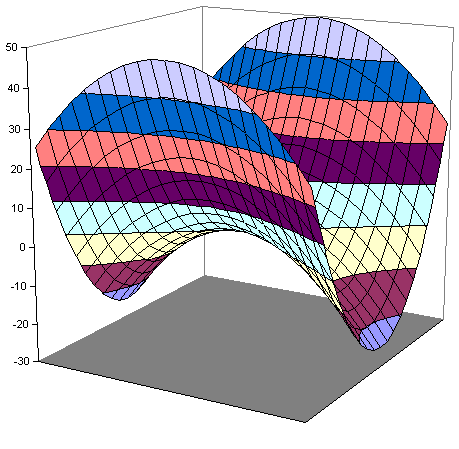
Fall 3a: $a < 0, \ b>0$ (Beispiel: $y= -1\cdot x_1^2 + 2\cdot x_2^2$)

Fall 3b: $a > 0, \ b<0$ (Beispiel: $y= 1\cdot x_1^2 - 2\cdot x_2^2$)

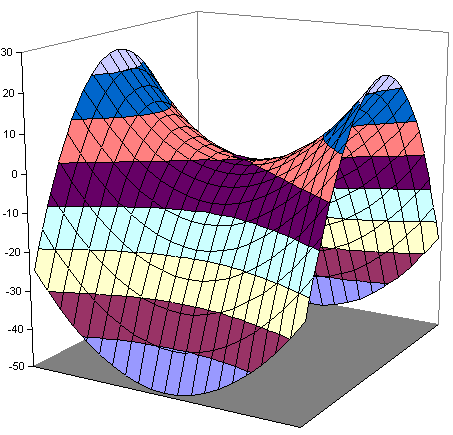
b. Notwendige Bedingungen für einen stationären Punkt: $$\left.\begin{matrix}{\partial f\over \partial x_1}\hfill &= &2ax_1 \hfill &\buildrel \rm ! \over = 0\cr\cr {\partial f\over \partial x_2}\hfill &= &2bx_2\hfill &\buildrel \rm ! \over = 0\end{matrix}\right\} \ \Longrightarrow x_1 = x_2 = 0 $$ Der einzige stationäre Punkt liegt bei $\vec{x} = \vec{0}$.

c. Hinreichende Bedingungen $$\mathbf{H} = \begin{pmatrix}f_{11} &&f_{12}\cr\cr f_{21} &&f_{22}\end{pmatrix} = \begin{pmatrix}2a &&0\cr\cr 0 &&2b\end{pmatrix}$$ Zur Bestimmung der Definitheit der Hesse-Matrix {$\mathbf{H}$} untersuchen wir ihre Hauptminoren: $$ |\mathbf{H_1}| = 2a \qquad |\mathbf{H_2}| = \begin{vmatrix}2a & 0\\ 0&2b\end{vmatrix} = 4ab$$ Fall 1: $a>0, \quad b>0$
Dann gilt: $$|\mathbf{H_1}| = 2a > 0 \qquad |\mathbf{H_2}| = 4ab > 0$$ ${\rm\bf H}$ ist also positiv definit. $\Rightarrow$ Der stationäre Punkt ist ein Minimum.
Fall 2: $a< 0, \quad b < 0$ $$|\mathbf{H_1}| = 2a < 0 \qquad |\mathbf{H_2}| = 4ab >0$$ ${\rm\bf H}$ ist also negativ definit. $\Rightarrow$ Der stationäre Punkt ist Maximum.
Fall 3a: $a>0, \quad b<0$ $$|\mathbf{H_1}| = 2a > 0 \qquad |\mathbf{H_2}| = 4ab < 0$$ ${\rm\bf H}$ ist also indefinit. $\Rightarrow$ Der stationäre Punkt ist weder Maximum noch Minimum.
Fall 3b: $a<0, \quad b>0$ $$|\mathbf{H_1}| = 2a < 0 \qquad |\mathbf{H_2}| = 4ab < 0$$ ${\mathbf{H}}$ ist also indefinit. $\Rightarrow$ Der stationäre Punkt ist weder Maximum noch Minimum.