|
Eine Funktion ist genau dann quasi-konkav, wenn die Niveaumengen
\begin{equation*}
\{\underline{x} \vert f(\underline{x}) \ge k\}
\end{equation*}
für alle $ k\in \mathbb{R} $ konvex sind.
Im eindimensionalen Fall ist dies gleichbedeutend mit der Aussage,
dass die Niveaumenge ein Intervall ist.
Bemerkung
Die Konvexitätseigenschaft kann bei monotonen Transformationen verlorengehen. Die Quasikonkavität bleibt erhalten. |
Quasi-Konkavität von Funktionen |
|
In der nebenstehenden Abbildung
sieht man eine Funktion in Abhängigkeit von zwei Variablen, die
quasikonkav aber nicht konkav ist.
Dass sie nicht konkav ist, macht man sich leicht dadurch klar,
dass man auf der dargestellten Fläche den vorderen linken und den
hinteren rechten Punkt durch eine Gerade (in der Abb. blau
gezeichnet) miteinander verbindet. Diese Gerade würde zuerst
oberhalb der Fläche (in der Abb. als durchgezogene Linie
dargestellt) und dann unterhalb der Fläche verlaufen (als
gestrichtelte Linie dargestellt). Bei einer konkaven Funktion
dürfte die Gerade keinen Punkt oberhalb der Fläche aufweisen.
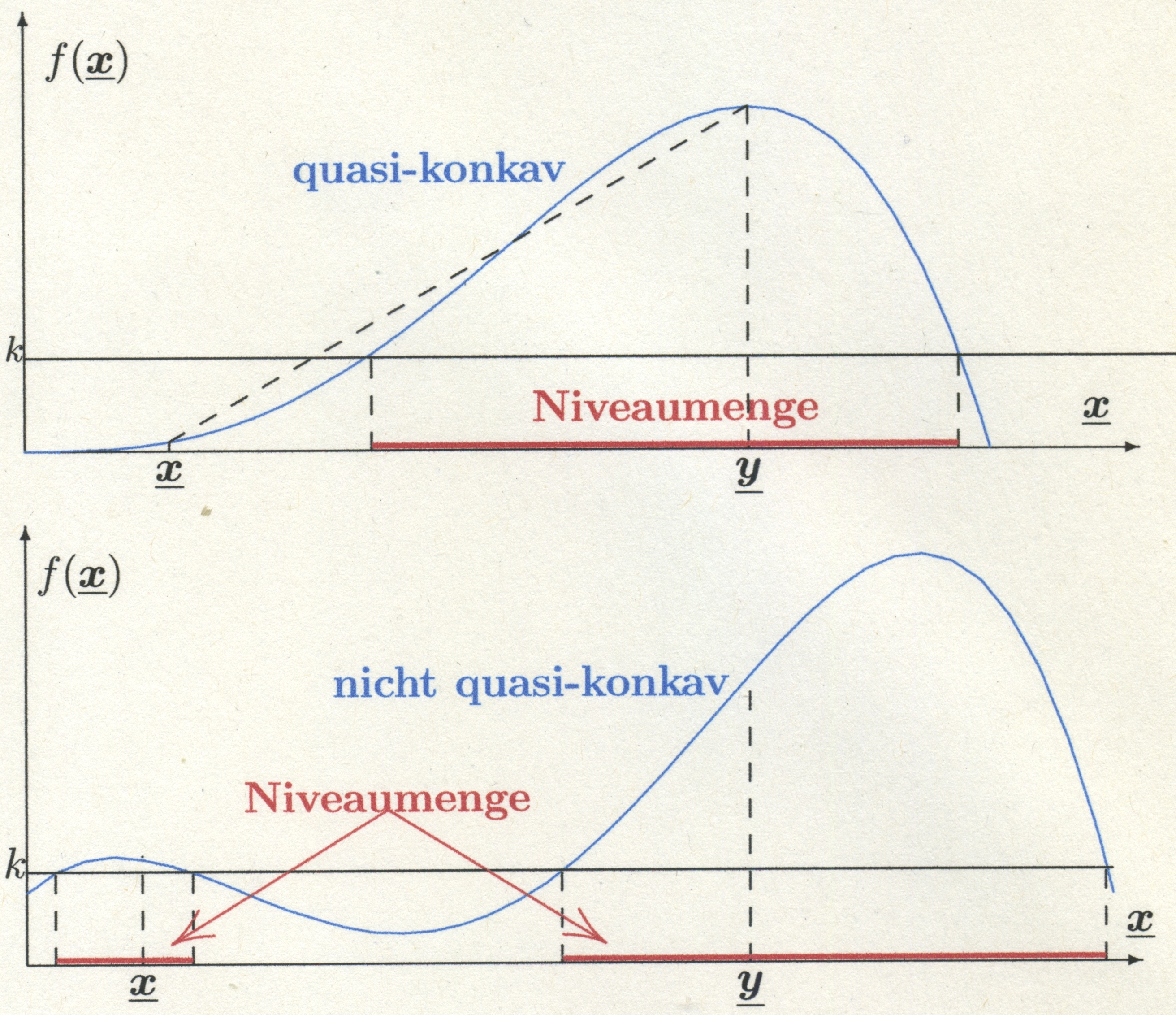
Diese Niveaumenge besteht aus allen $(x_1,x_2)$, deren Funktionswert größer gleich zwei ist. Grafisch ergibt sich diese Menge dadurch, dass die Höhenlinie der Höhe 2 von der Funktionsfläche senkrecht auf die Grundfläche projeziert wird (rote Kurve) und dann der Bereich auf der Funktionsfläche, der höher als zwei liegt, durch Schraffur in der Grundebene gekennzeichnet wird. In der Abbildung ist die Niveaumenge \begin{equation*} \{\underline{x} \vert f(\underline{x}) \ge k\} \end{equation*} für $k=2$ dargestellt. |
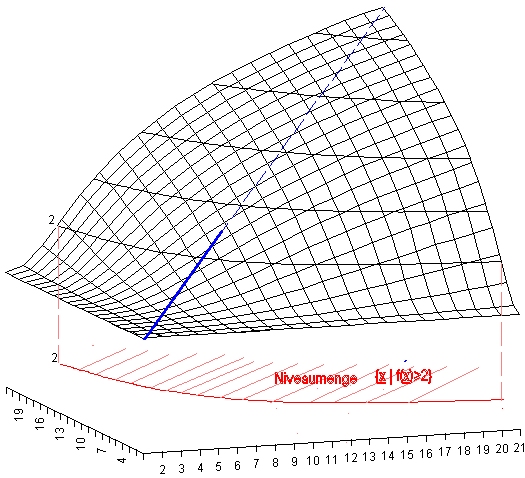
Quasi-konkave dreidimensionale Funktion |