Weist eine Funktion $f(x,y)$ an der Stelle $(x_0,y_0)$ ein relatives Extremum auf, dann existiert an dieser Stelle auch für die Vertikalschnitte senkrecht zur $x$-Achse sowie senkrecht zur $y-$Achse ein relatives Extremum.
Satz [Notwendige Bedingung für Extrema]
Besitzt eine nach beiden Variablen differenzierbare Funktion $f(x,y)$ an der Stelle $(x_0,y_0)\in \mathbb{D}$ ein relatives Extremum, dann sind die partiellen Ableitungen 1.Ordnung null: \begin{equation} f_{x}(x_0,y_0)=\frac {\partial f(x_0,y_0)}{\partial x}= 0 \end{equation} \begin{equation} f_{y}(x_0,y_0)=\frac {\partial f(x_0,y_0)}{\partial y}= 0 \end{equation}
Die partiellen Funktionen $f_x$ und $f_y$ haben an der Stelle $(x_0,y_0)$ eine waagerechte Tangente, die eine Tangentialebene aufspannen.

Definition: stationärer Punkt

Die Stellen $x,y \in \mathbb {D}$, in denen die partiellen Ableitungen 1.Ordnung $f_x$ und $f_y$ null sind, werden stationäre Punkte oder kritische Punkte der Funktion $f$ genannt.
Die Bedingungen, dass für die partiellen Ableitungen $f_{x},f_{y}=0$ gilt, sind zwar notwendige jedoch nicht hinreichende Bedingung für die Existenz eines Extremums an einem kritischen Punkt. Es gilt zwar, dass jeder Extrempunkt ein kritischer Punkt ist, der Umkehrschluss ist jedoch nicht immer gegeben. So ist es möglich, dass die partiellen Ableitungen $f_x$ und $f_y$ einer Funktion an der Stelle $(x_0,y_0)$ den Wert Null annehmen, ohne dass ein Extremum vorliegt. Als Beispiel sei hier auf den Sattelpunkt einer Funktion verwiesen.
Vgl. hierzu nebenstehende Abbildung.
Im Sattelpunkt weist der eine Vertikalschnitt immer ein relatives Minimum (Maximum) und der dazu senkrecht verlaufende andere Vertikalschnitt immer ein relatives Maximum (Minimum) auf. 	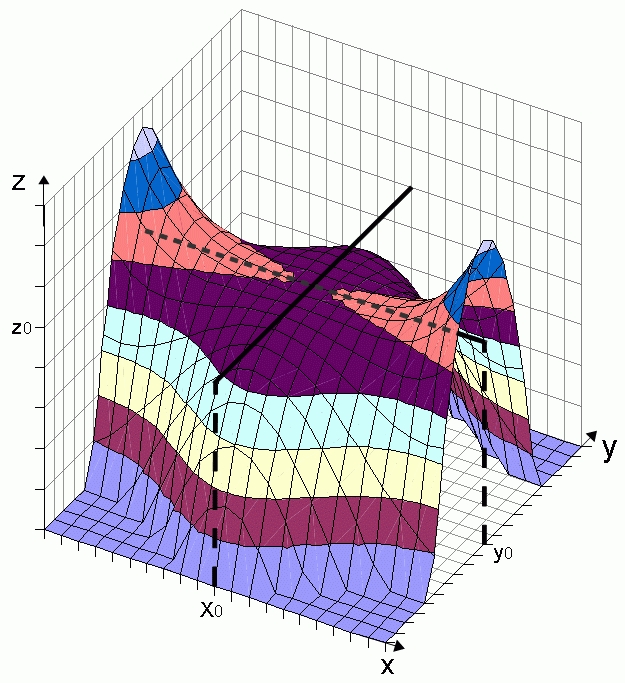	Sattelpunkt